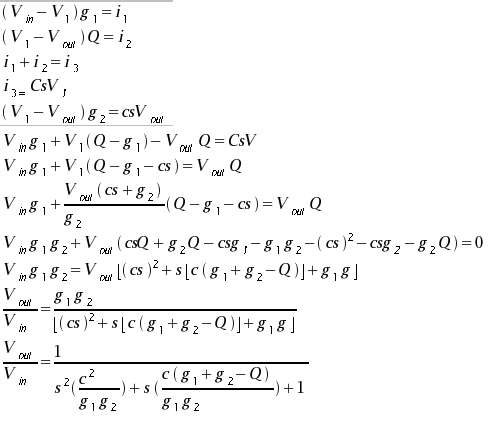Multi-Octave 4-Channel Tone
Synthesis With Magnitude Select
Layout of chip inside padframe
Objectives
Tone creation and synthesis is an important part of
Digital Signal Processing and has many applications. In our implementation, up
to four notes from a single octave can be 'played' at a time, each in its
respective channel. In addition, each channel has support for three different
magnitudes. The digital part of the design creates the desired tone frequency in
a square wave, which is sent to the analog part to be added to the other
channels. This result is then sent through a low-pass Butterworth filter to
remove as much of the harmonics as possible and create a sum of sine waves
output.
A Little Theory
Using Fourier Series expansion, it can be shown that
a square wave is actually the sum of a signal and its odd harmonics. Each of the
harmonics has a decreasing magnitude, inversely proportional to which harmonic
it is. The following picture shows this, using only the first four odd harmonics
in demonstration. The addition of more odd harmonics brings the composite
waveform nearer the shape of a perfect square wave. A perfect square wave is,
therefore, composed of an infinite number of odd harmonics.
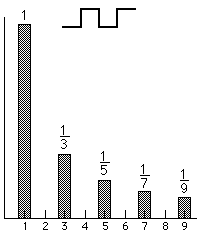
Odd sine harmonics
sum to create a square wave
Using a low pass filter
it is possible to remove all of the extra harmonics and get the original
frequency sine signal out. This is made easier by the fact that each successive
harmonic is a fraction of the original and only the odd harmonics exist. By
using a Butterworth filter we are able to achieve a slight increase in magnitude
of the original wave and an even further reduction of the odd
harmonics.
For a more in-depth discussion, see our References section [3].
Specifications
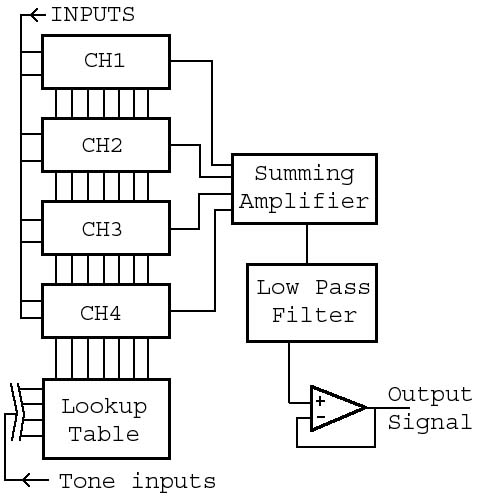
Top
level schematic of chip
Ultimately, our chip can be
broken down into two parts: a digital and an analog part. The digital part
consists of input logic, registers, counters, comparators, the lookup table and
the 'glue' to interface with the analog part. The analog part is the summing
amplifier for the four input channels, the Butterworth low pass filter and the
final op-amp voltage follower acting as a buffer for the output
signal.
Chip Pinout
| 1 |
Vref - on Butterworth filter (2.5V) |
40 |
Vbias - on Summing Amplifier (1.0V) |
| 2 |
Vn - Bias Volt. on NMOS trans. in summing Amp.
(3.0V) |
39 |
Vout - Output signal |
| 3 |
Vp - Bias Volt. on PMOS trans. in summing Amp.
(2.0V) |
38 |
VbiasOUT - on op-amp voltage follower (1.0V) |
| 4 |
Vda - Analog voltage source (5.0V) |
37 |
N.C. |
| 5 |
Gnd |
36 |
N.C. |
| 6 |
Q3 - for Butterworth filter, wc
= 1000Hz (453.1mV) |
35 |
N.C. |
| 7 |
Q2 - for Butterworth filter, wc
= 500Hz (422.5mV) |
34 |
N.C. |
| 8 |
Q1 - for Butterworth filter, wc
= 250Hz (392.4mV) |
33 |
N.C. |
| 9 |
g3 - for Butterworth filter, wc
= 1000Hz (476.3mV) |
32 |
N.C. |
| 10 |
g2 - for Butterworth filter, wc
= 500Hz (446.7mV) |
31 |
N.C. |
| 11 |
g1 - for Butterworth filter, wc
= 250Hz (415.8mV) |
30 |
N.C. |
| 12 |
V1 - small magnitude voltage (0.5V) |
29 |
N.C. |
| 13 |
V2 - normal magnitude voltage (1.0V) |
28 |
T3 - part of tone select |
| 14 |
V3 - large magnitude voltage (2.0V) |
27 |
T2 - part of tone select |
| 15 |
Vdd - Digital voltage source (5.0V) |
26 |
T1 - part of tone select |
| 16 |
OCT1 - part of octave select |
25 |
T0 - part of tone select |
| 17 |
OCT0 - part of octave select |
24 |
N.C. |
| 18 |
CH0 - part of channel select |
23 |
WRITE - write input data to selected channel |
| 19 |
CH1 - part of channel select |
22 |
CLK - 120KHz clock |
| 20 |
AMP1 - part of tone magnitude select |
21 |
AMP0 - part of tone magnitude
select |
Numbers in parenthesis are nominal voltages.
They may be modified post fabrication to achieve the desired operation
| Digital Input pins |
|
Analog Input pins |
|
Analog Output
pin |
Digital:
There are 12 pins that act as the digital input to
this chip. Ten of them are used to describe what type of tone is to be
generated, one is used for the input clock and the last pin is used for a write
signal. Their operations are described in the following tables:
| AMP1 |
AMP0 |
Description |
|
CH1 |
CH0 |
Description |
| 0 |
0 |
Turn off channel |
|
0 |
0 |
Write to Channel 1 |
| 0 |
1 |
Magnitude = V1 |
|
0 |
1 |
Write to Channel 2 |
| 1 |
0 |
Magnitude = V2 |
|
1 |
0 |
Write to Channel 3 |
| 1 |
1 |
Magnitude = V3 |
|
1 |
1 |
Write to Channel 4 |
| OCT1 |
OCT0 |
Description |
| 0 |
0 |
One octave above middle |
| 0 |
1 |
Middle Octave |
| 1 |
0 |
One octave below middle |
| 1 |
1 |
Not defined |
| T3 |
T2 |
T1 |
T0 |
Note |
| 0 |
0 |
0 |
0 |
B |
| 0 |
0 |
0 |
1 |
A#/Bb |
| 0 |
0 |
1 |
0 |
A |
| 0 |
0 |
1 |
1 |
G#/Ab |
| 0 |
1 |
0 |
0 |
G |
| 0 |
1 |
0 |
1 |
F#/Gb |
| 0 |
1 |
1 |
0 |
F |
| 0 |
1 |
1 |
1 |
E |
| 1 |
0 |
0 |
0 |
D#/Eb |
| 1 |
0 |
0 |
1 |
D |
| 1 |
0 |
1 |
0 |
C#/Db |
| 1 |
0 |
1 |
1 |
C |
We chose [131 - 247]Hz to be one octave below middle,
[262 - 494]Hz to be the middle octave, and [523 - 988]Hz to be one octave above
middle. The middle A was chosen to be 440Hz according to current standards. Each
of our octaves went from C to B. In the music world this means our three octaves
are C1 to B2, C2 to B3, and C3 to B4. The actual frequency values we used can be
found in a chart here: [1].
In order to achieve a square wave of proper frequency with a 50% duty
cycle, we modified an idea found in an IEEE paper: [2].
The basic idea is to divide the clock frequency by the desired frequency and use
this number as a value that a counter will count up to. These values are stored
in a lookup table according to the table listed above. The actual count values
were determined for the highest frequency octave because it would have the most
potential error. The lower and middle octaves use the same count values, but
have external clock splitters and internal logic to decide which clock it uses.
A comparator is used to compare the counter value with the desired value in the
lookup table. When the two values are equal, the comparator will output a clock
pulse and reset the counter. These pulses go into a flip flop set up as a clock
splitter which will create a clock output with a 50% duty cycle every two
pulses.
To choose an appropriate clock frequency, we went onto Digikey's
website and found the cheapest and most
common frequencies on the crystals it sold. We found about eight different
common frequency values from 40KHz to 250Khz, and wrote a simple matlab program
to determine which frequency would have the least squared error in approximating
the highest octave's frequencies. The frequency with the least error turned out
to be 120Khz, so we designed our lookup table with that value in mind.
Each 'channel' has a 7-bit counter, 8-bit comparator and 8-bit register.
The counter only needs 7 bits because in order to have the proper frequency
output, the lowest order bit is the clock itself, effectively making it an 8-bit
counter. The 8-bit register just stores the value of the count value found in
the lookup table every time the channel is written to. Each channel also has
another four flip flops to hold data on the octave and amplitude of each note,
which are used to determine which clock input to take and the magnitude of the
tone for the summing amplifier.

Layout
of each channel - with counter, comparator and registers
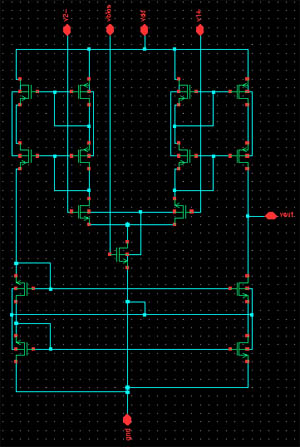
Analog:
The analog portion of this project can be further
split into two parts as well: the summing amplifer and the Butterworth low pass
filter. All of the important biasing and reference voltages for the analog parts
are off chip. This is so that if any unforseen problems occur, such as much
higher than expected intrinsic capacitances being formed for example, these
values will need to be changed to produce the desired operations.
 |
|
Layout of Op-Amp |
| Schematic of Op-Amp |
|
|
Our implementation of the Op-amp used
in the summing amplifier and the low pass filter was a modified version of one
given in the notes. We just cascoded the current mirrors and made the
transistors wider to support higher current flow.
 |
|
 |
| Schematic of Summing Amplifier |
|
Layout of Summing
Amplifier |
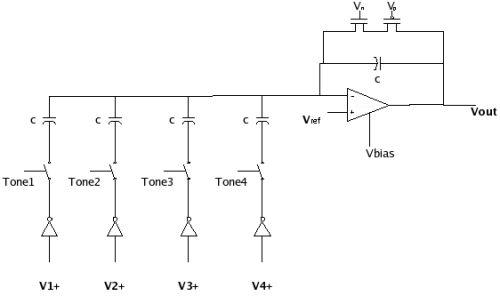
The summing amplifer
we used was also similar to one given in the class notes. Each wave input will
have its own frequency and amplitude, so we need to add the individual
amplitudes at their corresponding frequency rates. There are two pass gates per
tone, operated at the output clock frequency of each channel, which decide the
input to the summing amplifier. If the clock is high on a particular channel,
the appropriate voltage (given by the tone's magnitude, stored in each channel)
is applied to the input. If the clock is low, then Gnd is provided to the input.
Following the passgates is a set of four capacitor "banks," one for each
channel, which store the charge accumulated over a clock pulse. On the output,
charge redistribution occurs, so that all the voltage developed over each branch
will balance across all four branchs and yield one fourth of the total charge
sum. This voltage then connects to the negative terminal of the next part of
summing amplifier, the transconductance amplifier (a "sense amplifier").
Input into the transconductance amplifier is the average charge
summation at the negative terminal, and the reference voltage Vref at the
positive terminal. Vref is the voltage over which the output waveform will be
centered. For viewing purposes we chose Vref = 2.5V so the output wave would be
centered over a range of about 0 to 5.0V.
The feedback of the trans.
amp. is a capacitor in parallel with a resistor. Resistors are notoriously
difficult to implement in CMOS and maintain a linear transfer characteristic
along with not taking up too much space. The solution
was to use an NMOS and PMOS transistor in series. The gates of
these are attached to pins and have bias voltages of Vref plus/minus 0.5V
respectively. The resistor must be there to allow an actual DC voltage change at
Vout. The capacitor only passes the AC portion of the wave, so without both of
these components the summation could not occur.
In general this circuit
can be seen as an inverting amplifier with gain Cf (for the feedback capacitor)
divided by 4Ci (equivalent capacitance of four capacitors in parallel at the
input). The output in our case is the sum of the input tone amplitudes times the
gain added to a reference voltage. The output of this is then applied to the low
pass filter:
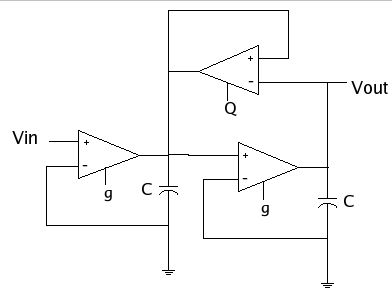
Schematic of 2nd order low pass
filter |
|
 |
|
|
Layout of 2nd order low pass
filter |
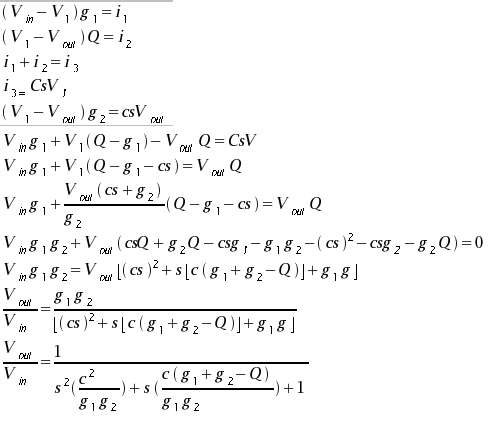
Derivation of Transfer Function |
|
To make this a Butterworth low pass
filter, the first thing we did was write down the transfer function of
this schematic. This is derived using the simple rules associated with
operational amplifiers discussed in our notes and in class.
The
definition of a butterworth filter describes the transfer function of the
filter as having two poles with negative real parts. They are complex and
are located at -135o and +135o in the complex plane.
So to avoid oscillation and have a real butterworth filter we had to fit
our equation to this constraint. |
|
|
|

Derivation of g to Q
relationship |
|
Using the -135o
and +135o pole location definition of a Butterworth filter, we
solved a general second order transfer function in terms of s and its
conjugate. We then set this value equal to the result obtained from the
derivation of the transfer function of our schematic and determined how
the g and Q were related.
We determined that Q is related to g
by a factor of two minus the square root of two. |
|
|
|
The next step was determining the
transconductance values (g and Q) for each cutoff frequency (fc).
These values were obtained by using the equations
(1) w=g/c
(2)
w=2*Pi*fc
(3) g = dI/(v2-v1)
in
conjunction with the transconductance amplifier characteristic plots of Iout vs
(v2-v1), and Iout as function of Vbias.
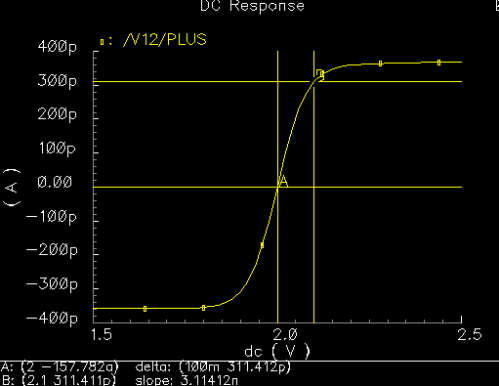 |
|
Here we plotted Iout as a function of v2. We went
about this plot by fixing v1 at 2V and then sweeping
v2. From this graph we observe the slope. The slope corresponds
to our transconductance value. What we aim for here is a large range over
which the slope (transconductance value) is constant. Our inputs will
depend on our tone amplitudes, values over which we have little control.
Therefore to be safe we played with values until we reached a comfortable
0.1V deviation range. Basically this means that as long as the difference
between our inputs (to trans amp) lie within the 0.1V range, the lowpass
filter will work correctly. |
| Solving for dI |
|
|
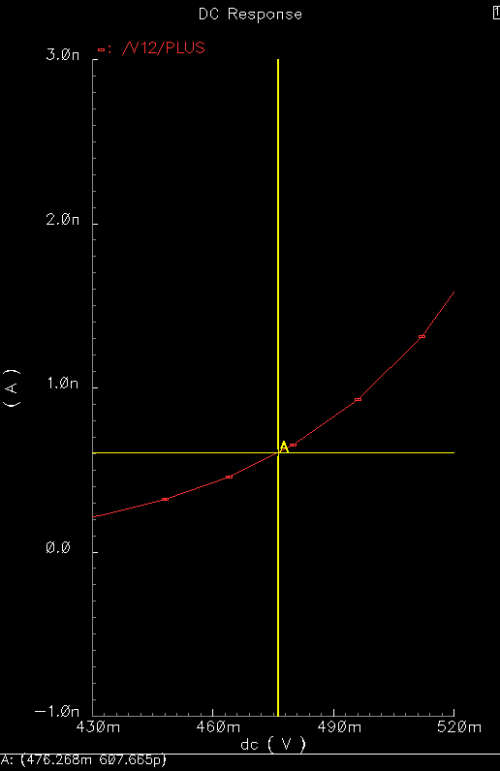 |
|
Using this dV and the relationship g=dI/dV, we then solve
for I. Now all we do is find the Vbias corresponding to I. This
is achieved by observing the Iout vs. Vbias
relationship of our transconductance. We trace our predetermined I to the
plotted curve. Our corresponding Vbias is the one we want.
|
| Solving for Vbias |
|
|
The Vbias solved for in the
last step will be the g values we want for each of the respective cutoff
frequencies in the low pass filter. We then solve for Q using the relationship
found earlier. All these values are located in the pinout table.
Results
The digital and analog parts of the chip were tested
seperately to assure proper operational behavior, then attached together on the
chip. To prevent unwanted operation of the analog components, we chose to use
two voltage sources. A digital source which would tolerate a certain amount of
bounce and wiggle, and a 'clean' analog source with a nice steady value. The
grounds were chosen to be the same, but only after surrounding all the digital
parts with a bulk and metal connection to ground. This should prevent the ground
bounce characteristic of rapidly switching digital components from excessively
affecting the analog parts of our chip.
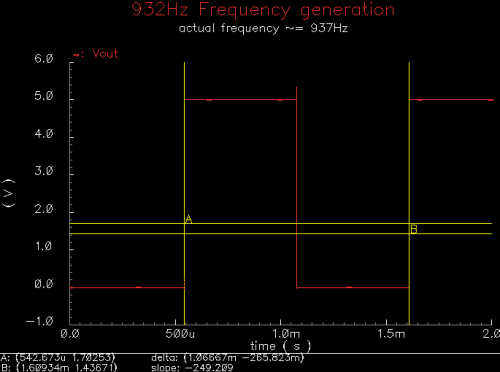 |
|
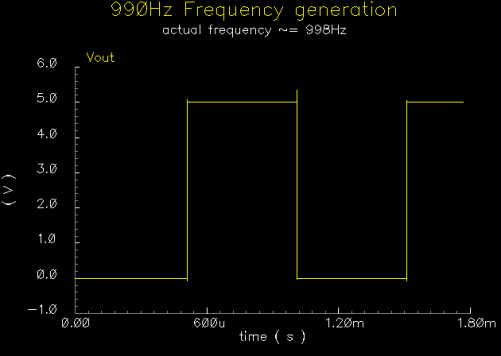 |
| 932Hz generated tone |
|
990Hz generated
tone |
The previous graphs show
two of the possible frequencies generated by the digital part of the chip. These
are two of the highest frequencies the chip will generate, and as such have the
highest possible error and take the least amount of time to simulate. As it was,
each of these two plots took about 25 minutes to simulate. We assume that since
these two frequencies output correctly and the logic controlling the clock input
works correctly, the other frequencies will generate correctly as well.
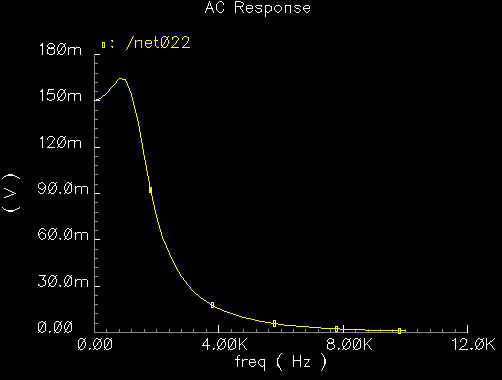
500Hz Transfer
Characteristic
This is the transfer characteristic of
the butterworth low pass filter for 500Hz. It has a peak at 500Hz and a fairly
sharp decline up to about 2000Hz.
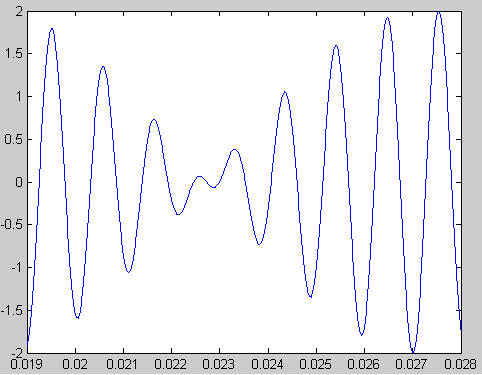 |
|
 |
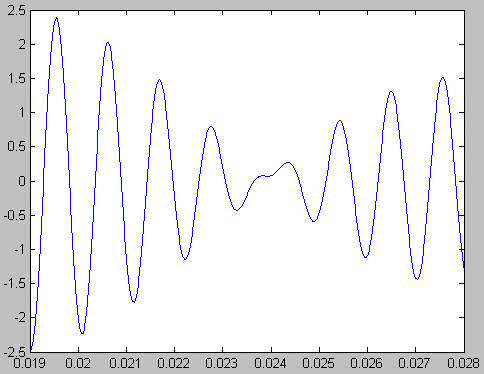
| Matlab Result |
|
Circuit
Result |
Adding up two
frequencies, 880Hz and 990Hz, we get the above waveform. On the left is the
'ideal' waveform graphed with Matlab, and on the right is the waveform that our
chip produces. As can easily be seen the results are very similar.
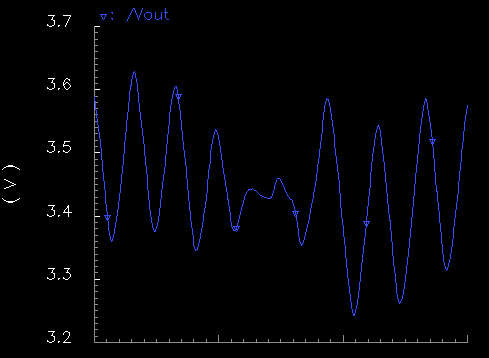
 |
|
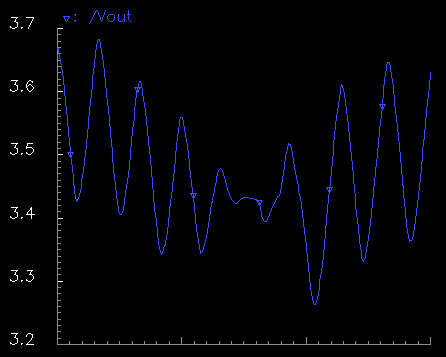 |
| Matlab Result |
|
Circuit
Result |
This is the sum of
three frequencies, 880Hz, 932Hz and 990Hz. Also, the 932Hz wave is half the
magnitude of the other two, as given with our implementation; i.e., the 932Hz
wave uses V1 as its magnitude voltage and the other two use V2 as their
magnitude voltage. This output doesn't quite follow the one from Matlab as
closely as the previous one, especially near the middle. Over a larger period of
time, the waveform does look more similar to the 'ideal' waveform. There is also
a noticeable phase shift on the signals from the chip which causes some of the
discrepancy. However, phase shifting a tone doesn't affect the overall sound to
a human ear so this output is acceptable.
References
[1] Abdullah, T. Yahay, "Music Scales - Frequency,
Notes, Octaves, ...," http://tyala.freeyellow.com/4scales.htm
[2] Wittman, B. A.;
Early, S.H.; Messerschmitt, D.G., "A Hardware Multitone Digital Frequency
Synthesizer", IEEE Transactions on Acoustics, Speech, and Signal Processing,
Vol. ASSP-27, No. 6, December 1979. pgs 804-809.
[3]
Higgins, Anna-Marie, "Fourier Synthesis" http://www.clubi.ie/amhiggins/fourier1.html